- AVL트리는 이진 검색트리로서 트리의 균형을 유지한다.
- 균형트리의 조건은 트리의 균형을 유지하기 쉬워야 하고 또한 트리의 깊이가 O(Log2n)을 보장
- 가장 간단한 균형트리의 조건으로서는 모든 노드의 왼쪽과 오른쪽 부속트리가 동일한 높이를 갖도록 하는 것이다.
- 그러나 이러한 조건을 만족하기 위해서는 2k-1 (k는 트리의 높이)개의 노드를 가지는 트리만이 가능하므로 현실적으로 유연하지 못한 구조
- AVL트리는 이진 검색트리와 동일한 구조를 가지며 단 한가지의 균형을 유지하기 위한 조건을 가진다. 즉, 모든 노드에서 왼쪽 부속트리와 오른쪽 부속트리 높이의 차이가 최대 1까지만 가능하다는 조건이다.
- 노드가 하나도 없는 비어있는 트리의 높이를 -1로 정의한다.
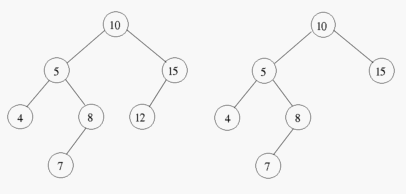
- 위의 그림에서 왼쪽의 트리는 AVL트리이지만 오른쪽의 트리는 AVL트리가 아니다.
- AVL트리를 구성하는 모든 노드에는 해당노드의 높이정보가 노드구조로서 저장된다.
- AVL트리의 높이는 아래의 식에 의해 계산될 수 있다.(n은 트리를 구성하는 노드의 개수를 나타낸다.)
1.44*log2(n+2)-0.328
- 그러나 실제상황에서의 AVL트리의 높이는 아래와 같다. 실험적으로 얻어진 것이다.
log2(n+1)+0.25
- AVL트리의 높이가 h일때 트리를 구성하는 최소숫자의 노드는 다음과 같이 구해진다.
N(h)=N(h-1)+N(h-2)+1
h가 0일때 N(h)=1, h가 1일 때 N(h)=2가 된다.
- 따라서 AVL트리에 대한 연산은 O(log2n)의 시간으로 수행될 수 있다.
- 이 경우 삽입연산은 예외이다. 삽입연산의 경우, 새로운 노드가 삽입되는 위치에서 루트노드까지의 경로 상에 존재하는 모든 노드의 균형정보가 업데이트되어야 한다.
- 또한 AVL트리의 특성을 유지하기 위해 만일 균형이 깨진다면 노드를 재구성하는 회전변형Rotation을 통해 균형을 유지해야 한다.
'사는 이야기 > 잡동사니들' 카테고리의 다른 글
| Saving private Ryan - Another war Behind story (0) | 2008.06.11 |
|---|---|
| Tom Otterness (탐 오더니스) 작품 Free Money (0) | 2008.04.27 |
| Saving Private ryan: another war (0) | 2008.04.10 |



